Altın Oran
Birçoğunuzun bildiği veya bir yerlerde duyduğu bir kavram Altın Oran. Peki nedir bu Altın Oran?
Altın oran kavramı insanlık tarihinde önemli bir yere sahiptir. Heykel, mimari, resim, estetik, fotoğraf, sinema, grafik tasarım gibi sanat dallarının vazgeçilmez unsurlarındandır. Sadece sanatın bir unsuru olarak değil, doğada canlı ve cansız varlıklarda da bu orana rastlanmak mümkündür. İnsan vücudu, deniz kabukları, çiçekler ve ağaç dalları gibi…
Altın oran kavramı; altın kesit, altın bölüm, altın sayı, altın kesim, altın anlam, altın nokta, kutsal bölümleme, kutsal oran gibi isimlerle de anılmaktadır.
Alman matematikçi, gökbilimci ve astronom Johannes Kepler; “Geometrinin iki büyük hazinesi vardır; biri Pythagoras’ın teoremi, diğeri de bir doğrunun Altın Oran’a göre bölünmesidir.’’
Altın oranın elde edilmesi için; bir doğru parçası iki parçaya ayrılır, küçük parçanın büyük parçaya oranı, büyük parçanın bütününe eşit olmalıdır. Bunun sonucunda 1,618 sayısı elde edilir.
Yunanlılar ve Mısırlıların mimarisinde, heykellerinde rastladığımız altın oranın en eşsiz örneği Mısır Piramitleridir diyebiliriz. Mısırlılar ‘Keops Piramidi’nin tasarlanmasında altın oranı kullanmışlardır. Mimar Sinan’ın çıraklık ve ustalık eserleri olan Süleymaniye ve Selimiye Camilerinin minareleri de altın oran özelliğini taşımaktadır.
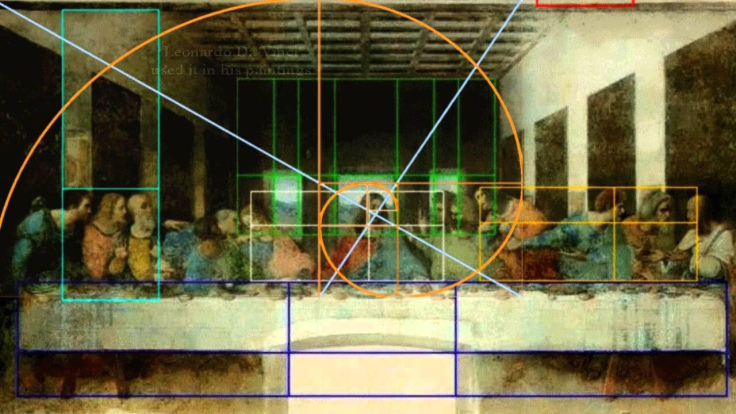
Altın oranı en çok kullanan sanatçı Leonardo da Vinci’dir diyebiliriz. Vinci’nin Son Akşam Yemeği’ adlı eserinde altın oranın olduğu alanlar aşağıda görülmektedir.
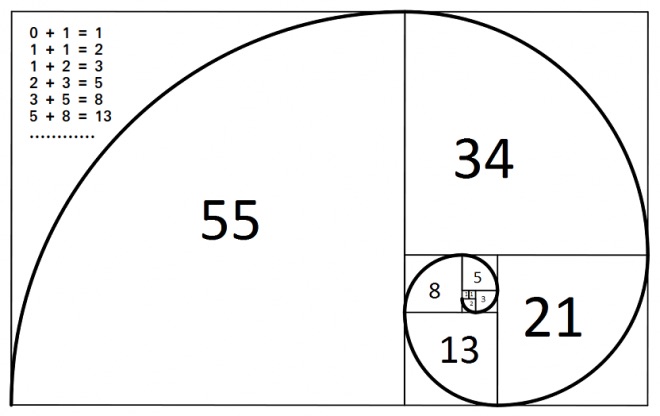
Fibonacci Spirali nedir?
Altın oranın en yaygın kullanımlarından biridir. Fibonacci Spirali de altın oran gibi bir çok yer de karşımıza çıkar. Bir deniz kabuğunda, papatyada, ayçiçeğinde hatta anne karnındaki cenin de bile.
Matematikçi Leonardo Fibonacci’den ismini alan bölümlemede her parçaya bir numara verilir. 1’den sonraki her sayı kendinden önce gelen sayıyla toplanır. Sekans içinde birbirini takip eden sayıların büyük olan sayının küçük sayıya oranı rakamların büyümesiyle altın orana yaklaşır. 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…
Örneğin; 5:3=1.666, 13:8=1.625, 13:8= 1.625 sayılar büyüdükçe sonuç 1,618’e yaklaşmaktadır. 1.618 sayısı da altın oranı vermektedir.

Fibonacci Spirali de altın oran gibi sinema ve fotoğraf sanatında sık sık karşımıza çıkar.
Birçok ünlü fotoğrafçı, fotoğrafçılıkta altın oranı kullanmalarıyla tanınır. Ansel Adams, çektiği manzara portrelerinde sık sık bu oranı kullandı.

Fibonacci Spiralinin en iyi örneklerine fotoğraf sanatçısı Henri Cartier Bresson’un fotoğraflarında rastlarız. Cartier-Bresson tüm kariyeri boyunca 50 mm lens kullandı, ekipmana daha az, kompozisyona daha çok odaklandı. Aşağıda kompozisyon tekniği olarak Fibonacci Spiralini kullanarak çektiği bir otoportre var.

Aşağıdaki Cartier-Bresson’ın çektiği fotoğraflarda görüldüğü gibi fotoğrafın en can alıcı noktaları bu spiralin içine yerleştirilmiştir.





Fotoğrafta Fibonacci Spiralini kullanmanın en kolay yolu, hareket halinde olan ya da olmayan nesnelerin sahnelerini çekmek ve konumuzu dokuzun dairesinde olacak şekilde yerleştirmektir.

1/3 Kuralı
Altın Oran kuralından ortaya çıkarılan bir kuraldır. 1/3 Kuralı kullanılarak oluşturulan fotoğrafların daha estetik ve etkileyici olduğunu söylemek mümkündür.

Fotoğrafta 1/3 Kuralını uygulamak için kadrajımızı yatay ve dikey olarak üçer eşit parçaya böleriz (hayali olarak). Bu çizgilerin birleşim noktalarına ana objemizi yerleştirerek etkileyici bir görüntü sağlayabiliriz. Tam bir Altın Oran olmasa bile bu işimizi görecek prensip 1/3 Kuralı olarak bilinir.
Günümüzde birçok fotoğraf makinesi vizörden baktığınızda (grid fonksiyonu açıksa) size bu bölünmüş alanları göstererek kullanmanıza yardımcı olmaktadır. Tabi ki tüm fotoğraflar bu şekilde olamaz; ama genel itibariyle bu kurala uygun kadrajlar gözümüze çok daha hoş görünecektir.
Etkileyici fotoğraflar çekmek istiyorsak altın oran kuralını kullanmak iyi bir tercih olacaktır…











